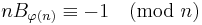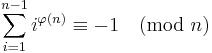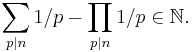Giuga number
A Giuga number is a composite number n such that for each of its distinct prime factors pi we have 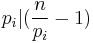 , or equivalently such that for each of its distinct prime factors pi we have
, or equivalently such that for each of its distinct prime factors pi we have 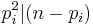 .
.
Another test for a Giuga number due to Takashi Agoh is: a composite number n is a Giuga number if and only if the congruence
holds true, where B is a Bernoulli number and 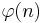 is Euler's totient function.
is Euler's totient function.
An equivalent formulation due to Giuseppe Giuga is: a composite number n is a Giuga number if and only if the congruence
and if and only if
The Giuga numbers are named after the mathematician Giuseppe Giuga, and relate to his conjecture on primality.
The sequence of Giuga numbers begins
- 30, 858, 1722, 66198, 2214408306, … (sequence A007850 in OEIS).
For example, 30 is a Giuga number since its prime factors are 2, 3 and 5, and we can verify that
- 30/2 - 1 = 14, which is divisible by 2,
- 30/3 - 1 = 9, which is 3 squared, and
- 30/5 - 1 = 5, the third prime factor itself.
The prime factors of a Giuga number must be distinct. If 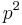 divides
divides  , then it follows that
, then it follows that 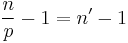 , where
, where 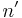 is divisible by
is divisible by  . Hence,
. Hence, 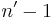 would not be divisible by
would not be divisible by  , and thus
, and thus  would not be a Giuga number.
would not be a Giuga number.
Thus, only square-free integers can be Giuga numbers. For example, the factors of 60 are 2, 2, 3 and 5, and 60/2 - 1 = 29, which is not divisible by 2. Thus, 60 is not a Giuga number.
This rules out squares of primes, but semiprimes cannot be Giuga numbers either. For if 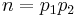 , with
, with 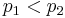 primes, then
primes, then 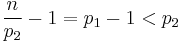 , so
, so 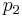 will not divide
will not divide 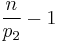 , and thus
, and thus  is not a Giuga number.
is not a Giuga number.
All known Giuga numbers are even. If an odd Giuga number exists, it must be the product of at least 14 primes. It is not known if there are infinitely many Giuga numbers.
It has been conjectured by Paolo P. Lava (2009) that Giuga numbers are the solutions of the differential equation n'=n+1, being n' the arithmetic derivative of n.
See also
References
- Weisstein, Eric W., "Giuga Number" from MathWorld.
- Borwein, D.; Borwein, J. M.; Borwein, P. B.; and Girgensohn, R. "Giuga's Conjecture on Primality." American Mathematical Monthly 103, 40-50, 1996.
- Giorgio Balzarotti, Paolo P. Lava - "103 curiosità matematiche", Hoepli, Milan 2010